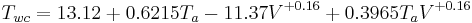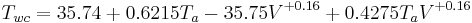Wind chill
Wind chill (often popularly called the wind chill factor) is the felt air temperature on exposed skin due to wind. The wind chill temperature is always lower than the air temperature, and the windchill is undefined at the higher temps (above 10 °C [50 °F]). Humidity on the skin can result in a higher felt air temperature, which is accurately termed the heat index (or humidex), and is used instead.
Contents |
Explanation
The human body loses heat through convection, evaporation, conduction, and radiation.[1] The rate of heat loss by a surface through convection depends on the wind speed above that surface: the faster the wind speed, the more readily the surface cools. For inanimate objects, the effect of wind chill is to reduce any warmer objects to the ambient temperature more quickly. It cannot, however, reduce the temperature of these objects below the ambient temperature, no matter how great the wind velocity. For most biological organisms, the physiological response is to maintain surface temperature in an acceptable range so as to avoid adverse effects. Thus, the attempt to maintain a given surface temperature in an environment of faster heat loss results in both the perception of lower temperatures and an actual greater heat loss increasing the risk of adverse effects such as frostbite and death.
Formulae and tables
Many formulae exist for wind chill because, unlike temperature, there is no universally agreed standard for what the term should mean. All the formulae attempt to provide the ability to qualitatively predict the effect of wind on the temperature humans perceive. Within different countries weather services use a standard for their country or region. U.S. and Canadian weather services use a model accepted by the National Weather Service. That model has evolved over time.
The first wind chill formulae and tables were developed by Paul Allman Siple and Charles Passel working in the Antarctic before the Second World War, and were made available by the National Weather Service by the 1970s. It was based on the cooling rate of a small plastic bottle as its contents turned to ice while suspended in the wind on the expedition hut roof, at the same level as the anemometer. The so-called Windchill Index provided a pretty good indication of the severity of the weather. In the 1960s, wind chill began to be reported as a wind chill equivalent temperature (WCET), which is theoretically less useful. The author of this change is unknown, but it was not Siple and Passel as is generally believed. At first, it was defined as the temperature at which the windchill index would be the same in the complete absence of wind. This led to equivalent temperatures that were obviously exaggerations of the severity of the weather. Charles Eagan[2] realized that people are rarely still and that even when it was calm, there was some air movement. He redefined the absence of wind to be an air speed of 1.8 metres per second (4.0 mph), which was about as low a wind speed as a cup anemometer could measure. This led to more realistic (warmer-sounding) values of equivalent temperature.
Original model
Equivalent temperature was not universally used in North America until the 21st century. Until the 1970s, the coldest parts of Canada reported the original Wind Chill Index, a three or four digit number with units of kilocalories/hour per square meter. Each individual calibrated the scale of numbers personally, through experience. The chart also provided general guidance to comfort and hazard through threshold values of the index, such as 1400, which was the threshold for frostbite. The change in the 1970s to the metric system units in Canada changed all the numbers, making it confusing and requiring that everyone recalibrate their personal wind chill scale. It should never have had units in the first place, as Siple later pointed out[3] for it was not a measure of human heat loss but simply a number proportional to human heat loss.
The original formula for the index was:
The general public seems to have been put off by the strange sounding units, either the old ones or the newer watts per square metre, and developed a strong preference for equivalent temperature, a deceptive simplification that only seems to be easier to understand. Even in the cold areas of Canada, broadcast media began to switch to the newer method of reporting after metrification.
North American wind chill index
In November 2001 the National Weather Service implemented the new wind chill index, used by the U.S. and Canadian weather services, which is determined by iterating a model of skin temperature under various wind speeds and temperatures. The model used standard engineering correlations of wind speed and heat transfer rate. Heat transfer was calculated for a bare face in wind, facing the wind, while walking into it at 1.4 metres per second (3.1 mph). The model corrects the officially measured wind speed to the wind speed at face height, assuming the person is in an open field.[6] The results of this model may be approximated, to within one degree, from the following formula:
- where
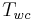 is the wind chill index based on the Celsius scale,
is the wind chill index based on the Celsius scale, 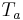 is the air temperature in °C, and
is the air temperature in °C, and 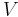 is the air speed in km/h measured at 10 metres (33 ft), standard anemometer height).[7]
is the air speed in km/h measured at 10 metres (33 ft), standard anemometer height).[7]
The equivalent formula in US customary units is:[8]
- where
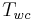 and
and 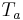 are measured in °F, and
are measured in °F, and 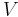 in mph.
in mph.
Click here [1] for a chart of windchills based on this formula.
Windchill Temperature is only defined for temperatures at or below 10 °C (50 °F) and wind speeds above 4.8 kilometres per hour (3.0 mph).[8]
As the air temperature falls, the chilling effect of any wind that is present increases. For example, a 16 km/h (9.9 mph) wind will lower the apparent temperature by a wider margin at an air temperature of −20 °C (−4 °F), than a wind of the same speed would if the air temperature were −10 °C (14 °F).
The method for calculating wind chill has been controversial because experts disagree on whether it should be based on whole body cooling either while naked or while wearing appropriate clothing, or if it should be based instead on local cooling of the most exposed skin, such as the face. The internal thermal resistance is also a point of contention. It varies widely from person to person. Had the average value for the subjects been used, calculated WCET's would be a few degrees more severe.
The 2001 WCET is a steady state calculation (except for the time to frostbite estimates[9]). There are significant time-dependent aspects to wind chill because cooling is most rapid at the start of any exposure, when the skin is still warm.
The exposure to wind depends on the surroundings and wind speeds can vary widely depending on exposure and obstructions to wind flow.
Australian Apparent Temperature
The Australian Bureau of Meteorology uses a different formula for cooler temperatures.[10]
The formula[11] is:
AT = Ta + 0.33e − 0.70ws − 4.00
Where:
Ta = Dry bulb temperature (°C) e = Water vapour pressure (hPa) ws = Wind speed (m/s) at an elevation of 10 meters
The vapour pressure can be calculated from the temperature and relative humidity using the equation:
e = rh / 100 * 6.105 * 2.718281828 ^ ( 17.27Ta / ( 237.7 + Ta ) ) Ta = Dry bulb temperature (°C) rh = Relative Humidity [%] ^ = means to the power of
The Australian formula includes the important factor of humidity and is somewhat more involved than the simpler North American model. However humidity can be a significant factor. The North American formula is designed mainly on the basis that it is expected to be applied at low temperatures, when humidity levels are also low, and also for much colder temperatures (as low as -50F). As these are qualitative models this is not necessarily a major failing.
A more exhaustive model (which factors in Wind Speed) was developed for the US Navy stationed in Parris Island in South Carolina. It was developed with a consideration for Heat Stroke due to the high humidity off the Island during summer months. It utilized three specialized thermometers.[12] This research is what the Australian Apparent Temperature formula was derived from.
Clothing, wet-cold and exposure duration
Wet clothing and the duration of a person's exposure to wind also affect the felt air temperature.[13] The wind chill formulae do not take account of the variation of clothing worn and how wet or dry a person is. The typical assumption is that a person will be properly dressed and dry. Models generally also assume that thermodynamic equilibrium exists, something that might not be the case if a person quickly run outdoors and back indoors, for example.
See also
References
- ^ http://books.google.com/books?id=q0QI19T_POkC&lpg=PA340&dq=%22evaporative%20cooling%22%20%22wind%20chill%22&pg=PA340#v=onepage&q&f=false
- ^ Eagan, C. (1964). Review of research on military problems in cold regions. C. Kolb and F. Holstrom eds. TDR-64-28. Arctic Aeromed. Lab. p 147–156.
- ^ Paul Siple, quoted in: Cold Injury, 1958, Steven Horvath editor, Josiah Macy Foundation, p 216.
- ^ *Woodson, Wesley E. (1981). Human Factors Design Handbook,page 815. McGraw-Hill. ISBN 0-07-071765-6
- ^ http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19690003109_1969003109.pdf
- ^ Osczevski, Randall and Maurice Bluestein. The New Wind Chill Equivalent Temperature Chart. Bulletin of the American Meteorological Society, Oct. 2005, p. 1453–1458.
- ^ Environment Canada (1 December 2003). "Wind Chill Science and Equations". http://www.msc.ec.gc.ca/education/windchill/science_equations_e.cfm. Retrieved 11 October 2006.
- ^ a b http://www.weather.gov/os/windchill/index.shtml
- ^ Tikuisis, P., and R. J. Osczevski (2002)Facial Cooling During Cold Air Exposure. Bull. Amer. Meteor. Soc. July 2003, p. 927–934
- ^ "Thermal Comfort observations.", Bureau Of Meteorology, Australia.
- ^ "The formula for the apparent temperature.", Bureau Of Meteorology, Australia.
- ^ "About the WBGT and Apparent Temperature.", Bureau Of Meteorology, Australia.
- ^ Thompson, R. L.; Hayward, J. S. (1996). "Wet-cold exposure and hypothermia: thermal and metabolic responses to prolonged exercise in rain". Journal of Applied Physiology 81 (3): 1128–1137. http://jap.physiology.org/cgi/content/abstract/81/3/1128. (as an example of this effect)
External links
- National Weather Service Wind Chill Temperature Index Table of wind chill temperatures
- National Science Digital Library - wind chill Temperature
- Environment Canada - Wind Chill
- Weather Images Wind Chill Chart and Introduction
- An Introduction to Wind Chill A lesson plan on wind chill
- A Cold Wind Blowing An article on wind chill and tables in SI units
- Wind Chill and Humidex Criticism about the use of wind chill and humidex
- An article about wind chill from The Canadian Encyclopedia
- Gorman, James (February 10, 2004). "Beyond Brrr: The Elusive Science of Cold". The New York Times. http://www.nytimes.com/2004/02/10/science/beyond-brrr-the-elusive-science-of-cold.html.
|
|||||||||||||||||
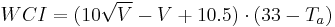
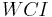 = Wind chill index, kcal/m2/h
= Wind chill index, kcal/m2/h = Wind velocity, m/s
= Wind velocity, m/s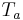 = Air temperature, °C
= Air temperature, °C